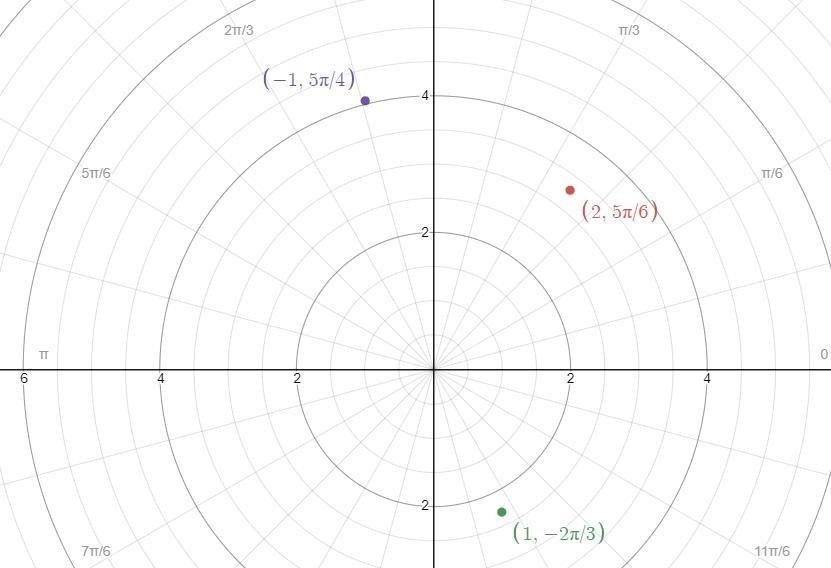
Plot the point whose polar coordinates are given. Then find two other pairs of polar coordinates of this point, one with r > 0, and one with r < 0.
(a) (2, 5pi/6)
(b) (1, -2pi/3)
(c) (-1, 5pi/4)
Answers
Answer:
The other pairs are:
[tex](a)\ (2, \frac{5\pi}{6}) \to[/tex] [tex](2, \frac{17\pi}{6})[/tex] and [tex](-2, \frac{23\pi}{6})[/tex]
[tex](b)\ (1, -\frac{2\pi}{3}) \to[/tex] [tex](1, \frac{4\pi}{3})[/tex] and [tex](-1, \frac{7\pi}{3})[/tex]
[tex](c)\ (-1, \frac{5\pi}{4}) \to[/tex] [tex](-1, \frac{3\pi}{4} )[/tex] and [tex](1, \frac{7\pi}{4})[/tex]
See attachment for plots
Step-by-step explanation:
Given
[tex](a)\ (2, \frac{5\pi}{6})[/tex]
[tex](b)\ (1, -\frac{2\pi}{3})[/tex]
[tex](c)\ (-1, \frac{5\pi}{4})[/tex]
Solving (a): Plot a, b and c
See attachment for plots
Solving (b): Find other pairs for [tex]r > 0[/tex] and [tex]r < 0[/tex]
The general rule is that:
The other points can be derived using
[tex](r, \theta) = (r, \theta + 2n\pi)[/tex]
and
[tex](r, \theta) = (-r, \theta + (2n + 1)\pi)[/tex]
Let [tex]n =1[/tex] ---- You can assume any value of n
So, we have:
[tex](r, \theta) = (r, \theta + 2n\pi)[/tex]
[tex](r, \theta) = (r, \theta + 2*1*\pi)[/tex]
[tex](r, \theta) = (r, \theta + 2\pi)[/tex]
[tex](r, \theta) = (-r, \theta + (2n + 1)\pi)[/tex]
[tex](r, \theta) = (-r, \theta + (2*1 + 1)\pi)[/tex]
[tex](r, \theta) = (-r, \theta + (2 + 1)\pi)[/tex]
[tex](r, \theta) = (-r, \theta + 3\pi)[/tex]
[tex](a)\ (2, \frac{5\pi}{6})[/tex]
[tex]r = 2\ \ \ \ \theta = \frac{5\pi}{6}[/tex]
So, the pairs are:
[tex](r, \theta) = (r, \theta + 2\pi)[/tex]
[tex](2, \frac{5\pi}{6}) = (2, \frac{5\pi}{6} + 2\pi)[/tex]
Take LCM
[tex](2, \frac{5\pi}{6}) = (2, \frac{5\pi+12\pi}{6})[/tex]
[tex](2, \frac{5\pi}{6}) = (2, \frac{17\pi}{6})[/tex]
And
[tex](r, \theta) = (-r, \theta + 3\pi)[/tex]
[tex](2, \frac{5\pi}{6}) = (-2, \frac{5\pi}{6} + 3\pi)[/tex]
Take LCM
[tex](2, \frac{5\pi}{6}) = (-2, \frac{5\pi+18\pi}{6})[/tex]
[tex](2, \frac{5\pi}{6}) = (-2, \frac{23\pi}{6})[/tex]
The other pairs are:
[tex](2, \frac{17\pi}{6})[/tex] and [tex](-2, \frac{23\pi}{6})[/tex]
[tex](b)\ (1, -\frac{2\pi}{3})[/tex]
[tex]r = 1\ \ \ \theta = -\frac{2\pi}{3}[/tex]
So, the pairs are:
[tex](r, \theta) = (r, \theta + 2\pi)[/tex]
[tex](1, -\frac{2\pi}{3}) = (1, -\frac{2\pi}{3} + 2\pi)[/tex]
Take LCM
[tex](1, -\frac{2\pi}{3}) = (1, \frac{-2\pi+6\pi}{3})[/tex]
[tex](1, -\frac{2\pi}{3}) = (1, \frac{4\pi}{3})[/tex]
And
[tex](r, \theta) = (-r, \theta + 3\pi)[/tex]
[tex](1, -\frac{2\pi}{3}) = (-1, -\frac{2\pi}{3} + 3\pi)[/tex]
Take LCM
[tex](1, -\frac{2\pi}{3}) = (-1, \frac{-2\pi+9\pi}{3})[/tex]
[tex](1, -\frac{2\pi}{3}) = (-1, \frac{7\pi}{3})[/tex]
The other pairs are:
[tex](1, \frac{4\pi}{3})[/tex] and [tex](-1, \frac{7\pi}{3})[/tex]
[tex](c)\ (-1, \frac{5\pi}{4})[/tex]
[tex]r = -1 \ \ \ \ \theta = \frac{-5\pi}{4}[/tex]
So, the pairs are
[tex](r, \theta) = (r, \theta + 2\pi)[/tex]
[tex](-1, \frac{-5\pi}{4}) = (-1, \frac{-5\pi}{4} + 2\pi)[/tex]
Take LCM
[tex](-1, \frac{-5\pi}{4}) = (-1, \frac{-5\pi+8\pi}{4} )[/tex]
[tex](-1, \frac{-5\pi}{4}) = (-1, \frac{3\pi}{4} )[/tex]
And
[tex](r, \theta) = (-r, \theta + 3\pi)[/tex]
[tex](-1, \frac{-5\pi}{4}) = (-(-1), \frac{-5\pi}{4}+ 3\pi)[/tex]
Take LCM
[tex](-1, \frac{-5\pi}{4}) = (1, \frac{-5\pi+12\pi}{4})[/tex]
[tex](-1, \frac{-5\pi}{4}) = (1, \frac{7\pi}{4})[/tex]
So, the other pairs are:
[tex](-1, \frac{3\pi}{4} )[/tex] and [tex](1, \frac{7\pi}{4})[/tex]
Related Questions
Use the figures to complete the statements proving the converse of the Pythagorean theorem.
Drag and drop a phrase, value, or equation into the box to correctly complete the proof.
Put responses in the correct input to answer the question. Select a response, navigate to the desired input and insert the response. Responses can be selected and inserted using the space bar, enter key, left mouse button or touchpad. Responses can also be moved by dragging with a mouse.
To prove the converse of the Pythagorean theorem, we can define a right triangle, Response area, with sides a, b, and x. Then, we will show that if △ABC is a triangle with sides a, b, and c where a² + b² = c², then it is congruent to △DEF and therefore a right triangle.
By the Pythagorean theorem, because △DEF is a right triangle, a² + b² = x².
If a² + b² = x² and a² + b² = c² , then c² = x². Further, since sides of triangles are positive, then we can conclude that c = x. Thus, the two triangles have congruent sides and are congruent.
If △ABC is congruent to a right triangle, then it must also be a right triangle.
Answers
To prove the converse of the Pythagorean theorem, we can define a right triangle Δ DEF with sides a, b, and x.
\What is the Pythagorean theorem?Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
We have,
ΔABC and ΔDEF
To prove the converse of the Pythagorean theorem, we can define a right triangle DEF with sides a, b, and x.
Thus,
ΔDEF is filled in the box.
Learn more about the Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ1
Someone please help with this!
Answers
Answer:
27/1
Step-by-step explanation:
3³=3·3·3=27
27=27/1
Which graph represents an exponential function?
Answers
Answer:
The answer to your question is the third one
Step-by-step explanation:
The first graph is the graph of a
The second graph is of a rational function
The third one is of an exponential function
vasta third one dzuh
Any graph that looks like the above (big on the left and crawling along the x-axis on the right) displays exponential decay, rather than exponential growth. For a graph to display exponential decay, either the exponent is "negative" or else the base is between 0 and 1.
Solve for l:
[tex]v = \frac{ \sqrt{l + t} }{2 \sqrt{l} } [/tex]
.....
Answers
Answer:
l = t/4v² - 1
Step-by-step explanation:
Given the expression
v = √l+t/2√l
We are to make l the subject of the formula as shown;
Cross multiply
2v√l = √l+t
Square both sides
(2v√l)² = (√l+t)²
4v²l = l+t
t = 4v²l - l
t = l(4v² - 1)
Divide both sides by 4v² - 1
t/4v² - 1 = l(4v² - 1)/4v² - 1
t/4v² - 1 = l
Swap
l = t/4v² - 1
Hence the required expression for l is t/4v² - 1
Graph the function n(x) = |x6|.
+Move Ray
-6
-4
-2
104
9
4
2
0
-2
Undo
2
4
Redo
6
x Reset
8
10
Answers
Answer:
x
)
=
2
x
4
−
3
x
+
3
f(x)=2x
4
−3x+3, then what is the remainder when
f
(
x
)
f(x) is divided by
x
−
1
x−1?
Find the exact value of the expression
Answers
Answer:
here is the correct answer
Find the sum: −11−7−3+1+⋯+225
Answers
Answer:
205
Step-by-step explanation:
Step-by-step explanation:
-11-7-3+1+225
-21+1+225
-20+225
205
Bernita and Rosalee are comparing their heights. Bernita is 1.63
meters tall. Rosalee is 19 centimeters shorter than Bernita.
What is Rosalee's height in centimeters?
Answers
Answer:
1.44
Step-by-step explanation:
1.63-.19= 1.44
If you save up $100 every 2 weeks, how much money would you have in a year ?
Answers
alr! so we know that there are around 52 weeks in a year (not counting leap years). and you save up 100 bucks every 2 weeks. then to find the answer, we do...
100(52/2)
100(26)
= $2600
youre welcome!
y≥ −4x+10
Hello, I’m having trouble the the following question above. Can you help me please?
The question asks to name the A and B points
A: ( , )
B: ( , )
Answers
I'm assuming x and y intercepts which would be (2.5,0) and (0,10)
A reporter for a student newspaper is writing an article on the cost of off-campus housing. A sample was selected of 10 one-bedroom units within a half-mile of campus and the rents paid. The sample mean is $550 and the sample standard deviation is $60.05. Provide a 95% confidence interval estimate of the mean rent per month for the population of one-bedroom units within a half-mile of campus. Assume that population is normally distributed.
Answers
Answer:
(507.05, 592.95)
Step-by-step explanation:
Given data:
sample mean = $550, sample standard deviation S = $60.05
95% confidence interval , n = 10
For 95% confidence interval for the mean
mean ± M.E.
where M.E. is margin of error = [tex]t_{n-1}, \alpha/2\times\frac{S}{\sqrt{n} }[/tex]
Substituting the values in above equation
[tex]=t_{10-1}, 0.05/2\times\frac{60.05}{\sqrt{10} }[/tex]
= 2.62×18.99
=42.955
= 550±42.95
=(507.05, 592.95)
Worked Example:
Select all the expressions that have the same value as 4 1/2% of 50.
A. 0.045x50
B. 4.5%x50
C. 43%x50
D. 4.5x50
E. 0.45x50
F. 412x50
Answers
Answer:
Options A and B------------------------------------------
4 1/2% of 50 is 4.5% of 50 which is same as:
4.5% × 50or substituting % with 1/100,
4.5/100 × 50 = 0.045 × 50The matching choices are A and B.
PLEASE HELP, ASAP. I WILL MARK YOU BRAINLIEST‼️
Answers
Which is 3 logx + 4 log(x-2) written as a single logarithm?
logx (x - 2)
logx(x-2)
b. 12 logx(x - 2)
d. 12 logx(x-2)
Answers
Answer:
The answer is [tex]12\log{(x(x-2))}[/tex]
Step-by-step explanation:
Exponential property of logarithm:
We have that:
[tex]a \log{x} = \log{x^{a}}[/tex]
Sum of logarithms:
We have that:
[tex]\log{a} + \log{b} = \log{ab}[/tex]
Applying the exponential property:
[tex]3\log{x} = \log{x^3}[/tex]
[tex]4\log{(x-2)} = \log{(x-2)^4}[/tex]
So
[tex]3\log{x} + 4\log{x-2} = \log{x^3} + \log{(x-2)^4}[/tex]
Additive property
[tex]\log{x^3} + \log{(x-2)^4} = \log{x^3(x-2)^4} = \log{(x(x-2))^12}[/tex]
Exponential property:
[tex]\log{(x(x-2))^12} = 12\log{(x(x-2))}[/tex]
The answer is [tex]12\log{(x(x-2))}[/tex]
Kenny loves to drink milk. He drinks 20 quarts of milk in 5 weeks. How many quarts of milk will Kenny drink in 12 weeks?
Answers
Answer:
32 mutipliy 20 and 5
Step-by-step explanation:
please help me to solve this
Answers
Answer:
Below in bold.
Step-by-step explanation:
First find the height by use Pythagoras theorem on the right triangle:
h = sqrt (5^2 - 4^2)
= sqrt 9
= 3.
Volume of the prism = area of the triangle * length
= 1/2 * 3 * 4 * 10
= 1/2 * 12 * 10
= 60 cm^3.
Total area = area of 2 triangles + area 0f 3 rectangles
= 2 * 1/2 * 3 * 4 + 3 * 10 + 4 * 10 + 5 * 10
= 12 + 30 + 40 + 50
= 132 cm^2.
evaluate the following polynomial when x = - 3
+6x² – 3x+5
2x
Answers
Answer:
-93
Step-by-step explanation:
Substitute by - 3 instead of X
what is the slope of the table below? 3/8 15/12 9/10 0/7
Answers
The slope of the table below? 3/8 15/12 9/10 0/7 is 23.8
What is slope?Slope is defined as the rate of change of y with respect to x. Invariably, it it the rise in y over the run in x. put differently, slope is increase over increase in x
The slope of a line is defined
S= (increase in y)/(Increase in x) = Δy/Δx
Slope = (0/7 - 18/12) ÷ (9/10 -3/8)
Slope = 15/12 ÷ 42/80
Simplify the fractions to have
Slope = 15/12 * 80/42
The slope = 1200/504
Slope of the table is given as 23.4
Conclusively, the table gives us a slope approximately 23
Learn more about slope on https://brainly.com/question/3605446
#SPJ1
express each number as a product of two fractions 1/5
Answers
Answer:
Theres nothing to solve for wheres the numbers?
Step-by-step explanation:
A box office sold 147,523 tickets for an auto race.
Of this number, 68,724 tickets were for adults.
The rest were children's tickets.
How many children's tickets were sold?
78,709
81,799
121,201
Answers
Answer:
78,799 children's tickets
Step-by-step explanation:
147,523 total tickets, 68,724 adult tickets
Subtract to find amount of children's tickets:
147,523-68,724 = 78,799
What is the range of the function x is 0 and y is 40
Answers
Answer:
range is y-coordinates so it should be 40
Step-by-step explanation:
domain is x-coordinates
can someone please help me on this question?
Answers
Answer: D
Step-by-step explanation:
If the graph is shifted 5 units down, each output value should decrease by 5.
find the volume of each figure
Answers
Answer:
1) 17.5×14×64
→ 1568 in³2) volume= 0.5×3.6×10×5=
→ 903) d= 13, r=13/2= 6.5, h= 19
→ v= πr²h→ π(6.5)²×19→ 2521.91 mm³4) Base Area= a+b/2×h
→ (37+15)/2×25.7 cm²→26×25.7 cm²→ 668.2 cm²height= 20cmvoulme = 668.2×20→ 13364 cm²5) L×W×H
→ 25×7×18→ 175×18→ 3150 ft³6) v=πr²h
→ π(3.2²)(8)→ 81.92π→ 257.36 km²[tex]------------[/tex]
hope it helps...
have a great day!!
[tex] \huge \boxed{1}[/tex]
→17.5 × 14 × 6.4
→1568 in³
[tex] \huge \boxed{2}[/tex]
→0.5 × 3.6 × 10 × 5
→90 m³
[tex] \huge \boxed{3}[/tex]
→ Diameter = 13 mm
→ Radius = 13/2 = 6.5
→ Height = 19 mm
→Volume => πr²h
=> 22/7 × (6.5)² × 19
=> 2521.91 mm³
[tex] \huge \boxed{4}[/tex]
→ Base Area → a+b/2×h
→ (37+15)/2×25.7 cm²
→26×25.7 cm²
→ 668.2 cm²
(height= 20cm)
→volume => 668.2×20
→13364 cm²
[tex] \huge \boxed{5}[/tex]
→Area→ L × B × H
→ 25×7×18
→ 175×18
→ 3150 ft³
[tex] \huge \boxed{6}[/tex]
→Volume → πr²h
→ π(3.2²)(8)
→ 81.92π
→ 257.36 km²
[tex] \boxed{Extra-Information}[/tex]
Always divide the diameter with 2 to get the radius.Volume is expressed in cube³ unit.[tex] \bold \green{TheExtraterrestrial}[/tex]
Kind of stuck any tips would also help!!
Answers
Answer:
Step-by-step explanation:
You must place in the question sign box the value of x that is above the question sign box because you are trying to fill out the y row.
Example: y=[tex]-\frac{0}{3} +2[/tex]= -0+2=2
Answer:
Step-by-step explanation:
tip:
plug the x values from the table ( the top row values ) into the equation
in this case its 0
BOX 1:
[tex]-\frac{0}{3} +2\\[/tex]
0 divided by anything = 0
so, 0 + 2 = 2
box 1 = 2
BOX 2:
[tex]-\frac{3}{3} +2[/tex]
3 div by 3 = 1 ( in this case negative 1 )
so, -1 + 2 = 1
box 2 = 1
BOX 3:
[tex]-\frac{6}{3} +2[/tex]
6 div by 3 = 2 ( in this case negative 2)
-2 + 2 = 0
box 3 = 0
Which list classifications for the figure
Answers
Answer: I think you forgot to post the picture
Step-by-step explanation:
Write two numbers that are opposites and more than 6 units away from 0.
Answers
Answer:
-7, 7
Step-by-step explanation:
Opposites are basically two numbers that are at different sides of the number line. For example, -2 and 2 are opposites because they are the same distance away from 0 on a number line making them opposites. To make an opposite just take a positive number, and then add a negative to it. (8, -8) Hope that helps :)
Please help giving brainliest please
Answers
In ΔABC, the measure of ∠C=90°, AB = 86 feet, and CA = 61 feet. Find the measure of ∠A to the nearest degree.
Answers
Answer:
<A=45°
Hope this helps you
Answer:
45
Step-by-step explanation:
What is the distance, rounded to the nearest tenth, between the points (-2,4) and (6,-4)?
Answers
HOPE ITS HELP
What is the gravitational potential energy of a 55-kg person that has climber a 4,000 meter tall mountain?
Bonus: if one snickers bar is 1,100,000 joules of energy, how many snickers bars would provide enough fuel to climb the mountain ?
Answers
Answer:
2156000 J.
Bonus: 2 snickers bar
Step-by-step explanation:
Applying
P.E = mgh................. Equation 1
Where P.E = Gravitational potential energy, m = mass of the person, h = height of the mountain, g = acceleration due to gravity.
From the question,
Given: m = 55 kg, h = 4000 m
Constant: g = 9.8 m/s²
Substitute these values into equation 1
P.E = (55×4000×9.8)
P.E = 2156000 J.
If one snikers bar is 1100000 J of energy,
Then, (2156000/1100000) snickers bar would be enough to climb the mountain
Number of snickers bar = (2156000/1100000) = 1.96 ≈ 2